How to find mean, median, mode and standard deviation in a continuous frequency table?

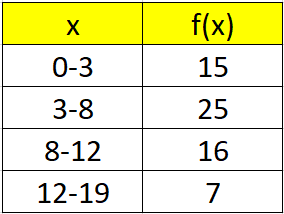
Let’s assume we have this table:

At first, we’d build an aiding table to assist and simplify all the calculations;

There’s the table:

The mean is calculated as it is calculated for discrete tables.

The mode is usually the mid-point of the class with the highest density (d); in some cases, it has a specific formula, but generally, it’s just the mid-point of the class with the highest level of density;

In this case: the highest density is for the 1^st and the 2^nd classes, so the we have 2 modes: 1.5 and 6.5.

Median:

Usually, the median is calculated using this formula:

At first, we need to decide, what is the relevant class for the median, and then – we have to implement the formula on the specific interval.

In our case, there are totally 63 respondents, so we’re looking for the value positioned at the 31.5^th position.

This can be found at the 2^nd interval (3-8).

That is the relevant value:

So, the interpretation for the result we got, is that 50% of the respondents has a value of 6.3 or less, and the rest of the 50% percent, have a value of 6.3 or more.

As for the standard deviation – the calculation is basically identical to the discrete case:

As for the variance – the calculation is identical, only without the root;

The inter-quartile-range (The IQR):

The IQR is the difference between the 25^th and the 75^th percentiles, or in other words: the mid 50% of the distribution.

That’s the calculation: