A geometric distribution is a distribution in which there is a series of repeated and independent trials (Bernoulli trials with a chance of success or failure), with a fixed chance of success (P).
Unlike the binomial distribution, which also consists of a series of Bernoulli trials, the geometric distribution has one success and it only occurs at the end. When success comes – the series of experiments ends.
Geometric distribution is infinite, meaning there is a chance of success the first time, the second time, the third time, the tenth time, the hundredth time, etc.
Mathematically we will define the distribution with a chance of success P, therefore with a chance of failure is 1-P.
The chance of success the K time is:

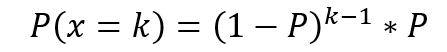
Expected value of number of trials until a success arrives:

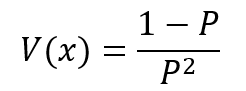
Question for example:

On his day off, John free throws with a chance of success of 0.82.

1. What is the probability that he will succeed the 4th time?
2. What is the chance that he will succeed at least the 3rd time?
3. What is his expectation of success?
4. What are the variance and standard deviation of his success?

Answer:

Part 1:

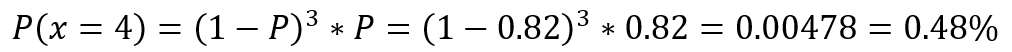
Part 2:

Part 3:

Part 4: